2.7 KiB
2.7 KiB
heap sort algorithm
Introduction
- Algorithme de classement in-place d'un tableau en le divisant en deux sous-tableaux contenant les éléments classés et non
classés,
- Efficace : O(nlog(n)) où n correspond au nombre d'éléments à classer,
- Le éléments non classés sont organisés dans une heap data structure,
- A chaque étape, l'élément max/min se trouvant à la racine du heap est déplacé dans le sous-tableau des éléments classés jusqu'à ce qu'il ne reste qu'un élément dans le sous-tableau des éléments non classés,
Organisation des éléments dans le tableau
Implémentation
from typing import Any, List
def heap_sort(array: List[Any]):
build_max_heap(array)
# start with the ending index all the way to 0
for end_index in range(len(array)-1, 0, -1):
swap(array, 0, end_index)
# reduce heap size by 1
# sift down the value we just swapped
heapify(0, end_index - 1, array)
# return array
def build_max_heap(array: List[Any]):
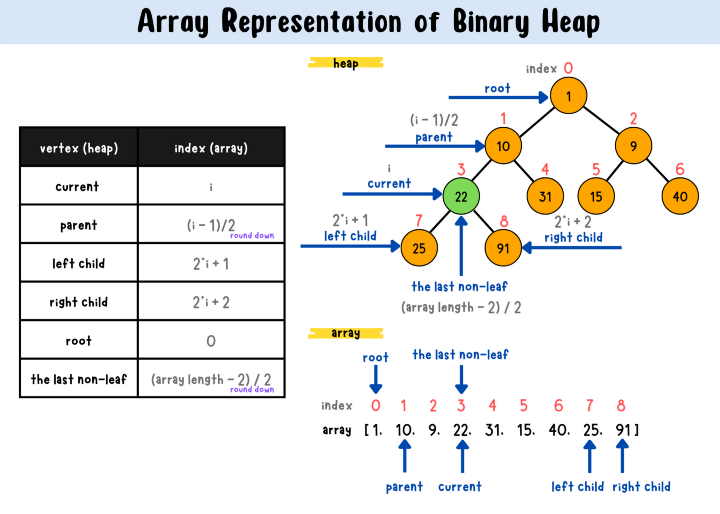
last_non_leaf_node_index = (len(array) - 2) // 2
for index in range(last_non_leaf_node_index, -1, -1):
heapify(index, len(array)-1, array)
# sift down
def heapify(current_index: int, end_index: int, array: List[Any]):
left_child_index = 2 * current_index + 1
while left_child_index <= end_index:
right_child_index = 2 * current_index + 2 if (2 * current_index + 2 <= end_index) else -1
largest_child_index = left_child_index
if right_child_index != -1 and array[left_child_index] < array[right_child_index]:
largest_child_index = right_child_index
if array[current_index] < array[largest_child_index]:
swap(array, current_index, largest_child_index)
current_index = largest_child_index
left_child_index = 2 * current_index + 1
else:
return
def swap(array: List[Any], i: int, j: int):
array[i], array[j] = array[j], array[i]
array = [1, -15, 22, 40, 9, 91]
print(f"Before sorting: {array}")
heap_sort(array)
print(f"After sorting: {array}")Before sorting: [1, -15, 22, 40, 9, 91] After sorting: [-15, 1, 9, 22, 40, 91]